本章我们先介绍软件测试的基本概念。为什么需要测试软件?一个测试软件如何运转的?如何判断测试是否成功?如何判断是否测试足够?在本章中,我们将回顾这些重要的概念,并同时熟悉Python的基本用法。
简单的测试
让我们先从一个简单的例子开始,当你希望实现平方根函数 时(让我们暂时假设环境没用这一个小功能)在研究了Newton-Raphson方法之后,提出了以下Python代码,通过my_sqrt()函数计算平方根。
def my_sqrt(x):
"""Computes the square root of x, using the Newton-Raphson method"""
approx = None
guess = x / 2
while approx != guess:
approx = guess
guess = (approx + x / approx) / 2
return approx
现在,让我们看看此功能函数是否真正按照规范执行。
了解python
如果您不熟悉Python,则可能首先必须了解以上代码的功能。这里非常推荐Python教程,以了解Python的工作原理。对于初学者来说,理解python代码最重要的是以下三个:
Python通过缩进构造程序,因此函数和
while主体是通过缩进来定义的;Python是动态类型的,这意味着变量的类型像
x,approx或guess在运行时才被确定。大多数的Python的句法特征是由其他语言启发的,如控制结构(
while,if),等号(=),或比较(==,!=,<)。
这样,你已经可以理解上面的代码是做什么:用开始guess的x / 2,它计算好近似approx直到值approx不再改变,这是最终返回的值。
运行功能函数
为了确定my_sqrt()是否正常工作,我们可以使用一些值对其进行测试。例如x = 4,对此它将产生正确的值:
my_sqrt (4 )
2.0
上面的上部my_sqrt(4)是Python解释器的输入,默认情况下对它进行运行,下部(2.0)是其输出。我们可以看到my_sqrt(4)产生正确的值。
这同样适用于x = 2.0:
my_sqrt (2 )
1.414213562373095
调试功能函数
为了解my_sqrt()内部运行方式,一种简单的策略是在关键位置插入print()语句。例如,您可以记录值approx,以查看每次循环迭代如何逐步接近实际值:
def my_sqrt_with_log(x):
"""Computes the square root of x, using the Newton–Raphson method"""
approx = None
guess = x / 2
while approx != guess:
print("approx =", approx) # <-- New
approx = guess
guess = (approx + x / approx) / 2
return approx
my_sqrt_with_log(9)
approx = None
approx = 4.5
approx = 3.25
approx = 3.0096153846153846
approx = 3.000015360039322
approx = 3.0000000000393214
3.0
这样我们就可以观察到每次运行时的内部细节,以排查问题。
检查功能函数
让我们回到测试。我们现在可以阅读并运行代码,但是上面的值my_sqrt(2)实际上正确吗?我们可以通过利用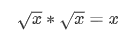
让我们来看看:
my_sqrt (2 ) * my_sqrt (2 )
1.9999999999999996
看起来确实有一些四舍五入上的错误出现了
现在,我们已经测试了上面的程序:我们已经在给定的输入上执行了该程序,并检查了其结果是否正确。在程序投入生产之前,这种测试是质量保证的最低限度。
自动化测试执行
到目前为止,我们已经手动测试了上述程序,即,手动运行它并手动检查其结果。这是一种非常灵活的测试方法,但是从长远来看,它效率很低:
手动测试,您只能检查非常有限的部分功能及其结果
对程序进行任何更改后,您必须重复测试过程
这就是为什么自动化测试非常有用的原因。一种简单的方法是让计算机首先进行计算,然后让计算机检查结果。
例如,这段代码自动测试
![]()
:
result = my_sqrt(4)
expected_result = 2.0
if result == expected_result:
print("Test passed")
else:
print("Test failed")
Test passed
这个测试的好处是我们可以一次又一次地运行它,从而确保至少正确计算了4的平方根。但是,仍然存在许多问题:
单个测试需要五行代码
它不在乎舍入错误
它仅检查单个输入(和单个结果)
让我们一一解决这些问题。首先,让我们使测试更加紧凑。几乎所有的编程语言都可以自动检查条件是否成立,如果条件不成立则停止执行。这称为断言,对于测试非常有用。
在Python中,我们使用assert语句,如果条件为true,则什么也不会发生。(如果一切正常,则不应该出问题。)但是,如果条件评估为false,assert则会引发异常,表明测试刚刚失败。
在我们的示例中,我们可以assert轻松地检查是否my_sqrt()产生了上述预期结果:
assert my_sqrt(4) == 2
当您执行此行代码时,什么都不会发生:我们证明(或断言)我们确认了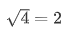 执行正确
执行正确
但是请记住,浮点计算可能会导致舍入误差。因此,我们不能简单地比较两个浮点数是否相等。因此,我们将确保它们之间的绝对差保持在某个阈值以下,通常表示为或epsilon。这是我们可以做到的:
EPSILON = 1e-8
assert abs(my_sqrt(4) - 2) < EPSILON
P.S. abs()求绝对值
我们还可以为此目的引入一个特殊功能,现在对具体值进行更多测试:
def assertEquals(x, y, epsilon=1e-8):
assert abs(x - y) < epsilon
assertEquals(my_sqrt(4), 2)
assertEquals(my_sqrt(9), 3)
assertEquals(my_sqrt(100), 10)
似乎可以工作,对吧?如果我们知道计算的预期结果,则可以一次又一次地使用此类断言,以确保我们的程序正确运行。
进一步生成测试
还记得 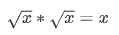 普遍恒成立吗?我们还可以使用一些值来明确地测试它:
普遍恒成立吗?我们还可以使用一些值来明确地测试它:
assertEquals(my_sqrt(2) * my_sqrt(2), 2)
assertEquals(my_sqrt(3) * my_sqrt(3), 3)
assertEquals(my_sqrt(42.11) * my_sqrt(42.11), 42.11)
似乎仍然有效,对不对?最重要的是通过 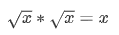 我们可以测试成千上万的值:
我们可以测试成千上万的值:
for n in range(1, 1000):
assertEquals(my_sqrt(n) * my_sqrt(n), n)
my_sqrt()用100个值测试需要多少时间?让我们来看看。
我们使用自己的Timer模块来测量花费的时间。为了能够使用Timer,我们首先导入我们自己的实用程序模块。
import bookutils
from Timer import Timer
with Timer() as t:
for n in range(1, 10000):
assertEquals(my_sqrt(n) * my_sqrt(n), n)
print(t.elapsed_time())
0.022911809000106587
10,000个值大约需要百分之一秒,因此单次执行my_sqrt()需要1/1000000秒或大约1微秒。
让我们重复随机选择10,000个值。Python的random.random()函数返回0.0到1.0之间的随机值:
import random
with Timer() as t:
for i in range(10000):
x = 1 + random.random() * 1000000
assertEquals(my_sqrt(x) * my_sqrt(x), x)
print(t.elapsed_time())
0.02770466199990551
一秒钟之内,我们测试了10,000个随机值,并且每次实际上都正确计算了平方根。只要对进行任何更改my_sqrt(),我们就可以重复进行此测试,每次都可以增强我们my_sqrt()没有隐患的信心。但是请注意,尽管随机函数在产生随机值方面没有偏好,但不太可能生成会极大改变程序行为的特殊值,我们将在下面稍后讨论。
在运行时验证
除了人为编写和运行测试外my_sqrt(),我们还可以将检查权限集成到实现中。 这样,将自动检查每次调用my_sqrt()。
这样的自动运行时检查非常容易实现:
def my_sqrt_checked(x):
root = my_sqrt(x)
assertEquals(root * root, x)
return root
现在,无论何时我们用my_sqrt_checked()…
my_sqrt_checked(2.0)
1.414213562373095
我们已经知道结果是正确的,并且对于每次新的成功计算都是如此。
如上所述,自动运行时检查假设有两件事:
必须能够制定这种运行时检查。始终有可能要检查具体的值,但是以抽象的方式制定所需的属性可能非常复杂。在实践中,您需要确定哪些属性最关键,并为它们设计适当的检查。另外,运行时检查可能不仅取决于本地属性,还取决于程序状态的多个属性,所有这些属性都必须确定。
必须能够负担得起此类运行时检查。在的情况下
my_sqrt(),运行花费不是很大;但是,即使经过简单的操作,如果我们不得不检查大型数据结构,那么检查的花费很快就会变得昂贵。在实践中,通常会在生产过程中禁用运行时检查,以确保可靠性为代价。另一方面,一套全面的运行时检查是发现错误并快速调试它们的好方法。您需要确定在生产期间仍需要多少种这样的功能。
系统输入与函数输入
在这一部分,我们会把my_sqrt()提供给其他程序员,然后他们可以将其嵌入他们的代码中。在某些时候,它必须处理来自第三方用户的输入,即不受程序员的控制。
让我们通过假设一个程序的输入为第三方字符串来模拟此系统输入:sqrt_program()
def sqrt_program(arg):
x = int(arg)
print('The root of', x, 'is', my_sqrt(x))
我们假设这sqrt_program是一个接受命令行输入的程序,如下所示:
$ sqrt_program 4
2
我们可以对sqrt_program()通过一些系统输入进行调用:
sqrt_program("4")
The root of 4 is 2.0
这会存在什么问题?问题在于我们不检查外部输入的有效性。例如sqrt_program(-1)尝试调用。怎么办?
实际上,如果您my_sqrt()使用负数调用,它将进入无限循环。由于技术原因,本章不能有无限循环(除非我们希望代码永远运行)。因此,我们使用一种特殊的with ExpectTimeOut(1)构造在一秒钟后中断执行。
from ExpectError import ExpectTimeout
with ExpectTimeout(1):
sqrt_program("-1")
Traceback (most recent call last):
File "<ipython-input-25-add01711282b>", line 2, in <module>
sqrt_program("-1")
File "<ipython-input-22-53e8ec8bb3ca>", line 3, in sqrt_program
print('The root of', x, 'is', my_sqrt(x))
File "<ipython-input-1-47185ad159a1>", line 7, in my_sqrt
guess = (approx + x / approx) / 2
File "<ipython-input-1-47185ad159a1>", line 7, in my_sqrt
guess = (approx + x / approx) / 2
File "ExpectError.ipynb", line 59, in check_time
TimeoutError (expected)
上面的消息是错误消息,表明出了点问题。它列出了错误发生时处于活动状态的函数和行的调用堆栈。最底部的行是最后执行的行;上面的几行代表函数调用–在我们的例子中,最大为my_sqrt(x)。
我们不希望我们的代码以异常终止。因此,在接受外部输入时,我们必须确保已对其进行正确验证。例如我们可以写:
def sqrt_program(arg):
x = int(arg)
if x < 0:
print("Illegal Input")
else:
print('The root of', x, 'is', my_sqrt(x))
然后我们可以确保my_sqrt()仅根据其规范进行调用。
sqrt_program (“ -1” )
Illegal Input
可是等等!如果sqrt_program()不使用数字调用怎么办?然后将尝试转换非数字字符串,这也会导致运行时错误:
from ExpectError import ExpectError
with ExpectError():
sqrt_program("xyzzy")
Traceback (most recent call last):
File "<ipython-input-29-8c5aae65a938>", line 2, in <module>
sqrt_program("xyzzy")
File "<ipython-input-26-ea86281b33cf>", line 2, in sqrt_program
x = int(arg)
ValueError: invalid literal for int() with base 10: 'xyzzy' (expected)
这是一个还会检查输入错误的版本:
def sqrt_program(arg):
try:
x = float(arg)
except ValueError:
print("Illegal Input")
else:
if x < 0:
print("Illegal Number")
else:
print('The root of', x, 'is', my_sqrt(x))
sqrt_program("4")
The root of 4.0 is 2.0
sqrt_program("-1")
Illegal Number
sqrt_program("xyzzy")
Illegal Input
现在我们已经看到,在系统级别程序必须保证能够正常地处理任何类型的输入,永远不会进入不受控制的状态。当然,这对于程序员来说是负担,他们必须努力使自己的程序在所有情况下都健壮起来。但是,这种负担在生成软件测试时会成为一个好处:如果程序可以处理任何类型的输入(可能带有定义良好的错误消息),就不容易出错。
测试的极限
尽管在测试方面付出了最大的努力,但请记住我们只是始终在检查功能是否有一组错误的输入。因此,可能总是存在未经测试的输入导致仍会失败。
某些情况下my_sqrt(),例如,计算 :
with ExpectError():
root = my_sqrt(0)
Traceback (most recent call last):
File "<ipython-input-34-24ede1f53910>", line 2, in <module>
root = my_sqrt(0)
File "<ipython-input-1-47185ad159a1>", line 7, in my_sqrt
guess = (approx + x / approx) / 2
ZeroDivisionError: float division by zero (expected)
到目前为止,在我们的测试中还没有检查这种情况,这意味着会出现出人意料地失败。但是,即使我们将随机生成器设置为产生0–1000000而不是1–1000000的输入,它偶然产生零值的机会仍然是百万分之一。如果对于几个单独的值,函数的行为完全不同,则纯随机测试几乎没有机会产生这些值。
当然,我们可以相应地修复功能,记录可接受的值x并处理特殊情况x = 0:
def my_sqrt_fixed(x):
assert 0 <= x
if x == 0:
return 0
return my_sqrt(x)
这样,我们现在可以正确地计算
assert my_sqrt_fixed(0) == 0
非法值会导致异常:
with ExpectError():
root = my_sqrt_fixed(-1)
Traceback (most recent call last):
File "<ipython-input-37-55b1caf1586a>", line 2, in <module>
root = my_sqrt_fixed(-1)
File "<ipython-input-35-f3e21e80ddfb>", line 2, in my_sqrt_fixed
assert 0 <= x
AssertionError (expected)
我们必须了解,尽管广泛的测试可以使我们对程序的正确性有很高的信心,但它不能保证所有将来的执行都是正确的。甚至检查每个结果的运行时验证也只能保证,如果产生一个结果那么结果将是正确的。但不能保证将来的执行不会导致检查失败。在撰写本文时,我相信函数my_sqrt_fixed(x)是正确的,但并不能100%确定。
经验教训
测试的目的是执行一个程序,以便我们发现错误。
测试执行,测试生成和检查测试结果可以自动化。
测试不完整; 它不提供100%保证代码没有错误的保证。
下一步
构建你自己的模糊测试——用随机输入测试程序。
来源:freebuf.com 2021-01-08 17:53:45 by: fstark










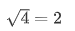
请登录后发表评论
注册