最近翻看PHP手册的时突然想到的一个点子，今天拿来复现一下觉得特别有趣，借此记录一下

案例

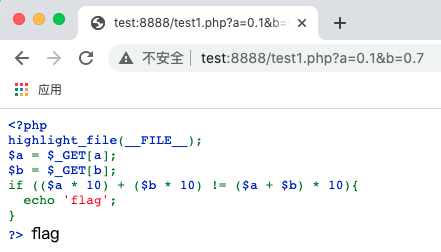
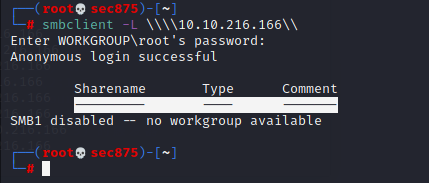
首先来看我测试时写的题目案例

<?php
highlight_file(__FILE__);
$a = $_GET[a];
$b = $_GET[b];
if (($a * 10) + ($b * 10) != ($a + $b) * 10){
echo 'flag';
}
?>

在数学公式中a*10+b*10=(a+b)*10是完全成立的 但在php中发生了意外，导致我们可以用一些手段来绕过这个公式

为什么在php中(0.1+0.7)*10=7？

我们查看php手册可以发现：

PHP 通常使用 IEEE 754 双精度格式，则由于取整而导致的最大相对误差为 1.11e-16。 十进制能够精确表示的有理数如 0.1 或 0.7，无论有多少尾数都不能被内部所使用的二进制精确表示，也因为存在这些误差，在进行数学运算时就会导致出现混乱的结果。首先我们需要了解什么是浮点数

浮点数

我们以双浮点数为例

1位符号位(E)

符号位：最高位表示数据的正负，0表示正数，1表示负数。

11指数位(Q)

指数位：表示数据以2为底的幂，指数采用偏移码表示

52位尾数(M)

尾数：表示数据小数点后的有效数字.

总共为64位

其实十进制0.1和0.7，对于二进制来说却是无限长的，由于浮点数存在位数长度的限制，就出现了误差

最后使得0.1+0.7=0.799999999999999……

这点其实不只是存在PHP语言中

python

JavaScript

分析

此时我们回到最上面的的问题

<?php
highlight_file(__FILE__);
$a = $_GET[a];
$b = $_GET[b];
if (($a * 10) + ($b * 10) != ($a + $b) * 10){
echo 'flag';
}
?>

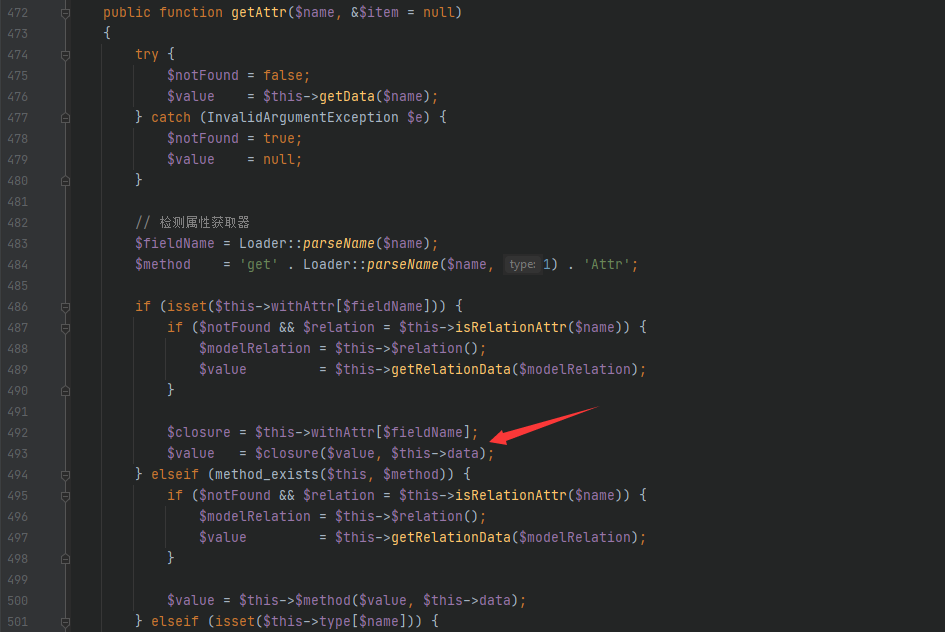
($a * 10) + ($b * 10)得到的结果是0.1*10+0.7*10=1+7=8最后结果是8

($a + $b) * 10得到的结果是0.1+0.7=0.79999999*10=7.9999999最后结果是7.9999999

相互比较出现了不等的问题，导致了绕过

总结

引用官方的一句话：永远不要相信浮点数结果精确到了最后一位，也永远不要比较两个浮点数是否相等。如果确实需要更高的精度，应该使用任意精度数学函数或者 gmp 函数。

来源：freebuf.com 2020-11-10 16:31:29 by: Thieves