前言
在安全攻防领域,攻击者常常会通过伪造浏览器信息(例如:userAgent、cookie等等)来模拟正常业务请求,达到自动化模拟重复请求的效果,进而制造暴力访问,信息遍历,羊毛撸取。这样的数据伪造方式影响恶劣,而且识别困难。本文就介绍一种浏览器基因技术集合机器学习算法来智能识别数据伪造的有效做法。
支持向量机(SupportVector Machine,SVM)
支持向量机即SVM法(Support Vector Machine),由Vapnik等人于1995年提出,具有相对优良的性能指标。该方法是建立在统计学习理论基础上的机器学习方法。通过学习算法,SVM可以自动寻找出那些对分类有较好区分能力的支持向量,由此构造出的分类器可以最大化类与类的间隔,因而有较好的适应能力和较高的分准率。该方法只需要由各类域的边界样本的类别来决定最后的分类结果。支持向量机算法的目的在于寻找一个超平面H(d),该超平面可以将训练集中的数据分开,且与类域边界的沿垂直于该超平面方向的距离最大,故SVM法亦被称为最大边缘(maximum margin)算法。待分样本集中的大部分样本不是支持向量,移去或者减少这些样本对分类结果没有影响,SVM法对小样本情况下的自动分类有着较好的分类结果。
SVM方法是通过一个非线性映射p,把样本空间映射到一个高维乃至无穷维的特征空间中(Hilbert空间),使得在原来的样本空间中非线性可分的问题转化为在特征空间中的线性可分的问题。简单地说,就是升维和线性化。升维,就是把样本向高维空间做映射,一般情况下这会增加计算的复杂性,甚至会引起“维数灾难”,因而人们很少问津。但是作为分类、回归等问题来说,很可能在低维样本空间无法线性处理的样本集,在高维特征空间中却可以通过一个线性超平面实现线性划分(或回归)。一般的升维都会带来计算的复杂化,SVM方法巧妙地解决了这个难题:应用核函数的展开定理,就不需要知道非线性映射的显式表达式;由于是在高维特征空间中建立线性学习机,所以与线性模型相比,不但几乎不增加计算的复杂性,而且在某种程度上避免了“维数灾难”。这一切要归功于核函数的展开和计算理论。
SVM里面最重要的两个点就是核函数及求解算法SequentialMinimal Optimization(简称SMO)。
核函数
1、方法原理
根据模式识别理论,低维空间线性不可分的模式通过非线性映射到高维特征空间则可能实现线性可分,但是如果直接采用这种技术在高维空间进行分类或回归,则存在确定非线性映射函数的形式和参数、特征空间维数等问题,而最大的障碍则是在高维特征空间运算时存在的“维数灾难”。采用核函数技术可以有效地解决这样问题。
设x,z∈X,X属于R(n)空间,非线性函数Φ实现输入间X到特征空间F的映射,其中F属于R(m),n<<m。根据核函数技术有:
K(x,z) =<Φ(x),Φ(z) >
其中:<, >为内积,K(x,z)为核函数。从上式可以看出,核函数将m维高维空间的内积运算转化为n维低维输入空间的核函数计算,从而巧妙地解决了在高维特征空间中计算的“维数灾难”等问题,从而为在高维特征空间解决复杂的分类或回归问题奠定了理论基础。
2、特点
核函数方法的广泛应用,与其特点是分不开的:
1)核函数的引入避免了“维数灾难”,大大减小了计算量。而输入空间的维数n对核函数矩阵无影响,因此,核函数方法可以有效处理高维输入。
2)无需知道非线性变换函数Φ的形式和参数.
3)核函数的形式和参数的变化会隐式地改变从输入空间到特征空间的映射,进而对特征空间的性质产生影响,最终改变各种核函数方法的性能。
4)核函数方法可以和不同的算法相结合,形成多种不同的基于核函数技术的方法,且这两部分的设计可以单独进行,并可以为不同的应用选择不同的核函数和算法。
3、常见的核函数
多项式核:![]()
高斯核(径向基函数):
径向基函数(Radical Basis Function,RBF)。径向基函数(Radical Basis Function,RBF)方法是Powell在1985年提出的。所谓径向基函数,其实就是某种沿径向对称的标量函数。通常定义为空间中任一点x1到某一中心x2之间欧氏距离的单调函数,可记作k(||x1-x2||),其作用往往是局部的,即当x1远离x2时函数取值很小。
线性核:
即是两个矩阵空间的内积。
SMO算法过程
SMO的主要两个步骤就是:
1、选择需要更新的一对α-i和α-j采取启发式的方式进行选择,以使目标函数最大程度的接近其全局最优值;
2、将目标函数对α-i和α-j进行优化,以保持其它所有α不变。 所需要的约束条件为:
核心算法实现
1、核函数变换,两种类型实现:线性及高斯核

2、SMO算法实现过程开源都比较多,这里由于篇幅有限不再赘述。
线上特性提取及实现
浏览器特性:
何谓浏览器特性。特性顾名思义就是无法更改,那么浏览器特性就是浏览器里面那些无法更改的信息。那么什么可以作为浏览器的特性呢?我们利用大数据进行分析发现:操作系统版本、硬件版本、浏览器内核、页面渲染时间、js执行性能这些因素单个都可以伪造,但是他们之间的关系很难伪造,我们就尝试通过这几个因素之间的关系分析来实现防伪造,如下图所示:

线上数据示例:

特性包括有:浏览器内核、浏览器名称及版本、运行平台、运行平台CPU版本、js执行时间、页面渲染时间等等,当然还可以扩展,例如浏览器的解析dom耗时、白屏耗时、domready耗时等等。而上图中以metric结尾的是相应特性的hash映射值。
正负样本选择:
正样本线上实时采集,负样本采取随机打乱组合的方式进行。
模块算法策略优化
在整个机器学习流程中我们添加了一个动态分界点计算及二次分类的做法,这个做法就是解决分类准确性问题,由于单一固定的分界点事先虽然可以确定,但是分类效果很差,所以我们依据分类后预测的结果值来进行动态选择,再进行二次分类。这个优化之后将系统的准确性从60%直接升为99%以上,效果显著。
实验过程及结果
我们线上采集10000条数据,并随机打乱伪造5000数据作为负样本,通过svm拟合得出一个预测值,并将预测值计算出正负样本的最大似然分界点,
再依据分界点将预测值进行二次分类。基本流程如下:

原始数据分布如下图所示:
 经过算法多次分类之后得到的结果如下:
经过算法多次分类之后得到的结果如下:


总结
本文主要介绍一种基于浏览器特性的防伪造算法,并且引入动态临界点策略验证,提升整体算法预测效果,现在该算法已上线应用在例如注册、登录,活动等业务场景下。本文同时旨在引入一种方客户端防伪造的做法,抛砖引玉,共同探索。
来源:freebuf.com 2019-04-11 10:47:43 by: flyking








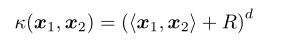
请登录后发表评论
注册