16位NE程序逆向调试：CrackMe012全破 – 作者:huluwa007

前言

CrackMe012,现在全网好像没有人发文全破的，能找到的唯一资料也就是反汇编代码的分析了，最终破解被精度误差给拦住了，这种底层不具备可行性的问题到底怎么解决呢？文章分为两部分，前部分先说环境的搭建和如何调试这个16位NE程序，以及反汇编代码研究算法，后部分是独稿，来解决这个一直悬而未决很多年的Crackme012。

准备

网盘链接: https://pan.baidu.com/s/1j_38rOvm83zoyTcJxutwXw提取码: awdv

【环境和工具】

win7/xp虚拟机环境
win95虚拟机环境
IDA
TRW2000（16位调试器）
CrackMe012

【学习层次】

能成功调试16位NE程序
静态+动态分析清楚算法
解决精度误差导致的无法破解的问题

详解视频

16位动态调试环境的搭建              00:00 至 00:18
逆向分析算法                       00:18 至 00:55
整理公式写注册机遇到精度难题        00:55 至 01:04
解决问题                          01:04 至 01:37

环境工具搭建

NE程序

我们接触比较多的都是PE程序，而这个是16位的NE，NE到底是什么，有兴趣的可以问百度，针对于我们要去处理的CrackMe012我们需要知道如何调试他即可，首先OD是无法使用的。

IDA可以正常分析，如图，可见是NE程序：

win95+trw2000动态调试

16位NE程序的调试需要了解以下几点：

16位动态调试工具是TRW2000；

16位NE程序运行环境最高是XP；

但XP虚拟机和TRW2000显示不出来（不知道为啥）；

最终我选择了win95+trw2000；

win98我没实验，应该也可以；

win95VM镜像文件在网盘，我用的是VM12；

直接打开就可以用，如果你非要自己装win95,其实由于需要虚拟启动盘，还是有些复杂的；

win95虚拟机在VM12里面，装了VMtools也是不能和物理机拷贝文件的；

所以把需要拷贝的TRW2000和CrackMe012做成了一个光盘映像；

加载入win95虚拟机，就可以了。

win95搭建好如下图：

光盘映像，拷贝到C盘即可，不要放桌面，TRW2000不太友好复杂路径。

win95系统映像和光盘映像在网盘

TRW2000的简单使用

TRW2000可不像OD那样好用，是DOS窗口程序，绝大部分功能是依赖于命令行操作，动态调试一个程序，最基础的几个功能，下断点，看内存数据，步过，步入，执行到指定地址等，下面就简单介绍这些功能的命令和快捷键。

以上功能的熟悉使用基本已经可以胜任这个CrackMe的分析了，再多的请去百度，顺便提一下，TRW2000貌似是看不了浮点寄存器，反正我是没调出来，正巧这次CrackMe还牵扯大量浮点数。

TRW2000调试CrackMe012

IDA静态分析，我们根据错误字符串定位到了关键代码块的入口点，如下图：

需要注意的是，IDA分析的比较精准，而载入TRW2000后，发现入口地址那一段代码识别的是有点问题的，由于头部一般都是一些初始化检查啥7的，没有实质代码，所以我们往下面一点下断点也没什么问题，从【0207】后识别的就没啥问题了，我们就在【0207】处下断点。

先打开trw2000,载入CrackMe012，如动图：

下断点，输入伪码，动态调试，如动图：

截至到此，虽然操作远不如OD那么爽朗，但是已经可以正规的动态调试了，动态调试的侧重点在于对静态分析验证，良好的基本功可以保证你在阅读反汇编代码静态分析的准确性，拿不准需要验证的地方当然还得依靠动态调试。下面部分就是静态分析结合动态验证后的分析结果，也就是这个CrackMe012的算法。

算法分析

整体流程图

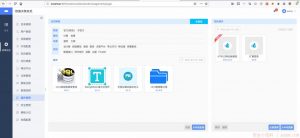
反汇编代码精解

判断字符串的长度，我们记输入的password为变量sP，长度是len。

一些值得初始化，定义个循环,循环长度是len。

所有sP的字符ASC码求和，是80位浮点型，记为ldSum。

cos(ldSum(sqrt(ldSumd1)+ln(ldSum/d2))+sin(len)cos(len*ldSum))

是不是得给高中数学复习一下才能看懂？

上面计算出来的值，转化位科学计数法的字符串，带上符号，E之前一共17位，我们记为变量S17。

下面的部分功能是根据S17重新摘要出一个新的字符串，长度9，我们记为S9，因为代码类似度极高，又长就不列举了，需要注意的是这一段，多少有些不一样。

整个循环控制数是从大到小的，也就是说大的先执行；

9块代码上面基本都是按照从大到小；

只有这块是0x2，是最小的，却代码顺序并不是最后；

不要被迷惑，虽然写在前面，但是执行是最后执行的；

而且这段代码跟其他的都不一样，其他的是在后方追加；

而这个是直接插在前面，也就是说这是实际的S9[1]；

其实这个时候就可以充分发挥动态调试的优点；

静态分析很容易出错，最后还是要去动态验证一下；

静态就像理论，动态就像实践，实际结果是检验分析是否正确的唯一标准。

具体这块特殊于其他八块的代码如下图：

最终静态结合动态验证后，得出如下表格：

S9序列	算法
1	S17[2]+0xA
2	S17[8]+0x3C
3	S17[17]+0x30
4	S17[16]+0x2A
5	S17[15]+0x35
6	S17[14]+0x2C
7	S17[13]+0x2F
8	S17[12]-0x15
9	S17[3]-0xD

复杂的计算工作基本完成了，后面就是根据计算结果的验证流程，这是第一重合规验证，要求：

sP[6] = S17[6]+0x16
sP[9] = S17[7]*2-9

这是第二重合规验证，首先对S9所有字符ASC求和，然后加上len,即输入的password的长度：

然后，要求上面计算的结果要等于S17[4]9+S17[5]4+20：

全部完了，我们开始整理最终的简化公式：

由于S9所有字符是通过S17的相应字符根据上换算表得来；

又由于最终对比值是S17[4]和S17[5]相关；

所以我们把S9所有字符的ASC值和全部换算为S17的相应字符。

最后整理的结果为：

S17[2]+S17[3]+S17[8]+S17[12]+S17[13]+S17[14]+S17[15]+S17[16]+S17[17]+270+len = 9S17[4]+4S17[5]+20

即等于：

S17[2]+S17[3]+S17[8]+S17[12]+S17[13]+S17[14]+S17[15]+S17[16]+S17[17]+250+len = 9S17[4]+4S17[5]

同时还要满足：

sP[6] = S17[6]+0x16
sP[9] = S17[7]*2-9

着手写注册机遇到难题

由于牵扯不太好逆推的数学运算，例如三角函数，对数运算等，所以我们基本的注册机思路是枚举注册机，要观测大量数据，所以我们不用MFC框架了，就用控制台程序来编写，便于观测数据！

从输入的password获得制式的17位字符串源码如下：

我们在CrackMe12中输入”12″，动态调试看看S17是多少，如下图：

可以看到是”-2.57875261112076″,我们在用我们的注册机计算一下，则是”-2.57875261112079″,出现了误差，如下图：

我们再以”123″作为password分别看看，如下：

发现误差更大，这下就没办法往下进行了，因为：

误差的根本可能来自48位浮点数这个过时的类型；

我们目前用的要么32位，要么64位，要么80位；

误差也可能来自于16位系统和32位系统的开发环境所利用的计算库本身的不同；

最关键误差出现在了17位长度之内，而后面的S17转S9是一定会涉及第12位到第17位；

这种底层的根本性障碍导致后面根本没有进行的必要了。

这里是分割线，目前我在网络上可以找到的关于CrackMe012的资料也就停止到这里了，也就是说这个CrackMe并没有最终破掉， 且看我如何把他解决掉！

打破常规 人机结合 抽丝剥茧 柳暗花明

既然遇到了这种过不去的坎，又不想放弃，那么就只有看看是否还有其他的路可走，我们整个算法分析的过程，涉及三个字符串，分别是sP,即输入框输入的password,也是我们最终的目标，第二个字符串是S17，由sP通过不可精确逆推的数学计算得到，第三个字符串是S9，通过S17固定位通过可逆推的简单加减法获得。我们分别详细梳理三个字符串，如下

sP即password

sP长度大于等于9（由存在sP[9]合规判断可知，至少9个字符）；

sP字符范围暂不确定（6.9位可以确定大概范围，但没突破性意义）；

sP通过不可以准确逆推的数学计算决定S17的值；

sP决定S17的核心变量仅仅是sP字符的和，即ldSum，而并不关心具体是什么字符（这一点至关重要，因为可以把穷举爆破的指数级次数直接降至计算机在1秒内可以完成的量级）；

sP间接决定S9，也就是sP间接决定最终程序弹框内容。

S17

S17是由三角函数cos得到，所以S17的实际数值取值范围是-1到1之间；

S17最终格式化输入字符串，第一位不是负号就是空格；

S17的2.3.8.12.13.14.15.16.17位通过简单固定的加减运算得到S9；

最终合规判断发生关系的是S17的第4.5位和S9；

也可以理解为最终发生关系的是S17的第4.5位和S17的第2.3.8.12.13.14.15.16.17位；

S17除了第1.3位不是数字，其他的都是数字，也就是说每一位ASC码范围只能是48-57。

S9

S9字符串可以逆推S17的2.3.8.12.13.14.15.16.17位；

逆向理解就是S9字符串字符受制于S17的2.3.8.12.13.14.15.16.17位，并且范围很小；

有了S17的2.3.8.12.13.14.15.16.17位可能算出S17的4.5位；

如果有了S17的2.3.4.5.8.12.13.14.15.16.17位后，最开始的误差问题可能就不是大问题了；

S9字符串的作用是作为破解后的弹框显示内容。

上面的这些梳理看完之后，是不是隐隐约约有柳暗花明的感觉，然而真正的破冰点只差一句话”要是能猜出来S9的内容“。

那么究竟猜出来S9的内容是否有可行性呢？看如下信息碎片：

S9一共九个字符；

S9是实质意思应该不是杂乱的字符，内容应该是表示注册成功的；

根据程序风格和代码风格，开发者应该有相当不错的基本功；

通过已知字符串的风格，开发者非常喜欢用标点，而且标点使用规范；

那么S9的最后一个字符根据开发者的心理行为特征大概率猜可能是个感叹号（这种难度的CrackMe成功拿下了，最终弹框字符串用感叹号是规范准确的使用，符合开发者的心理和行为侧写）。

S9根据算法和S17数字字符串的特点，归纳其字符范围如下表：

看到S9第9个字符是感叹号的时候，直觉告诉我一定是可行的，因为之前我忽略了S17[3]一定是小数点这个事实，对S9最后一位的判断纯属直觉的推测，然而事实证明推测是正确的，一种对路子的直觉油然而生。而然后根据这些字符范围，组合猜测到底是啥，反正我是靠直觉，30秒内就看出来了，如下图：

猜到了Cracked！！基本就从”柳暗花明”找到了”另一村”了。

S9有了，逆推S17相应位置，S17具体化为(X代表不确定数字)：

X9.XXXX6XXX659691

而算法公式：

S17[2]+S17[3]+S17[8]+S17[12]+S17[13]+S17[14]+S17[15]+S17[16]+S17[17]+250+len = 9S17[4]+4S17[5]

可以整理为：

731+len=9S17[4]+4S17[5]

那么我们来做一道小学奥赛题：

9X+4Y-Z=731，XYZ均为正整数，XY取值范围48-57，Z大于等于9，求X、Y、Z。

上面方程的唯一解是X＝Y＝57，Z=10，那么S17更具象为：

X9.99XX6XXX659691

同时知道password长度是10位。

看到了这样的S17那么上面提到的计算误差已经不是大问题了，因为可以人机配合的去筛选出真正的值，下面看源码：

当S17的值约等于0.999。

char szRes[100] ={0};
int i = 480;
while (i < 1221)
{
long double ldRes = GetS17bySum(i);
    sprintf(szRes,"%.17Lf\n",ldRes);
//x9.99xx6xxx659691
    //测试0.999
    if (szRes[2]==0x39 && szRes[3]==0x39 && szRes[4]==0x39)
{
   printf("%d,%s",i,szRes);
}
i++;
}
getchar();
return 0;

运行结果发现没有符合S17特征的：

那么再穷举当S17值约等于-0.999：

//十个字符长度的数字或字母组成的字符串asc码值的和是480-1220
 char szRes[100] ={0};
 int i = 480;
 while (i < 1221)
 {
 
 long double ldRes = GetS17bySum(i);
     sprintf(szRes,"%.17Lf\n",ldRes);
 //x9.99xx6xxx659691
    //测试-0.999
     if (szRes[3]==0x39 && szRes[4]==0x39 && szRes[5]==0x39)
 {
    printf("%d,%s",i,szRes);
 }
 i++;
 
 }
 getchar();
 return 0;

找到了匹配项，如下图：

这时候离最后成功仅仅差一步了，就是放入真正CrackMe012去验证，进行最后的梳理，如下：

筛选出的结果ldSum的值是1006，也就是10位password的所有字符asc码的和是1006；

第6位是S17[6]+0x16,即0x33+0x16=73,即字符是大写字母i；

第9位是S17[7]2-0x9,即0x382-0x9=103，即字符是’g’。

我们那么其他八位组合方式就多了，只要他们和加起来等于1006-73-103，即：

我这里选择gggggIgggm。

先看真正CrackMe012中的S17到底是多少：

可见符合我们的推算X9.99XX6XXX659691。

那么F5运行，激动人心的画面出现了：

最后我们再写一个逼格高一点，随机性强一点的注册机，源码如下：

void CCM002Dlg::OnOK() 
{
 // TODO: Add extra validation here
 
    char sP[11]={0};
 sP[5]=73;
 sP[8]=103;
 sP[0]=rand()%(110-97+1)+97;
 sP[9]=207-sP[0];
 sP[1]=rand()%(110-97+1)+97;
 sP[7]=207-sP[1];
 sP[2]=rand()%(110-97+1)+97;
 sP[6]=207-sP[2];
 sP[3]=rand()%(112-97+1)+97;
 sP[4]=209-sP[3];
    SetDlgItemText(IDC_EDIT2,sP);

最后在XP中运行测试，如下动图：

*本文作者：huluwa007，转载请注明来自FreeBuf.COM

来源：freebuf.com 2019-03-07 16:00:18 by: huluwa007