RSA加密解密原理深度剖析（附CTF中RSA题型实战分析）

*本文作者：Fly鹏程万里；本文属 FreeBuf 原创奖励计划，未经许可禁止转载。

前言

凡是从事信息安全领域的技术人才一定会与密码学打交道，而对于经常参与国内各大CTF大赛的各位技术人员而言密码学也是一个常见的题型，本文章就密码学中的RSA发展、RSA的数学基础理论、RSA的加密解密算法原理、CTF中的RSA题型剖析等多方面进行详细的分析讨论，希望对各位有所帮助。

RSA的发展

1976年，Diffie和Hellman发表了非对称密码的奠基性文章《密码学的新方向》，建立了公钥密码的概念。很多密码学家加入到了解决这个问题的行列当中。1978年，麻省理工学院的Rivest、Shamir和Adleman在他们的论文《获得数学签名和公钥密码系统的一种方法》中，实现了Diffie和Hellman提出的思想的一种算法，简称RSA，即为三个人名字的手字谜的缩写。这三个人中，Rivest和Shamir是计算机学家，负责提出解决方案，Adleman是数学家，负责指出方案的不足，让他们在错误的道路上少浪费时间。Rivest和Shamir花费了一年的时间尝试各种想法，Adleman也花了一年多的时间来一一击破。当他们失望的时候，Rivest终于找到了一种解决方案，这就是我们现在看到的RSA算法。他们获得了2002年的图灵奖。图灵奖是计算机最负盛名、最崇高的一个奖项，有“计算机界的诺贝尔奖”之称。Diffie和Hellman获得了2015年的图灵奖。

从RSA算法产生到现在，密码学家对该算法的安全性进行了广泛的研究和讨论，并且在实践中有了广泛的应用，比如：数字签名算法、身份认证算法等等，这些算法都是基于大数分解难题的算法（在后面的安全性部分会详细介绍）。

RSA的数学基础理论

素数（质数）、合数、互质数

素数：一个数如果除了1与它本身之外没有其他的因数，那么这个数就被称为素数（或者质数，取自英文单词prime的首字母）。

合数：如果一个数大于1，且该数本身不是素数，那么这个数就是一个合数。

互质数：如果两个整数a,b的最大公因数（greatest common divisor）为1，即gcb(a,b)=1，那么称a,b两数互质,。

欧拉函数值

设m为正整数，则1,2,3,4…….,m中与m互素的整数的个数记为，叫做欧拉函数，欧拉函数的值叫做欧拉函数值。

取模运算与同余的概念

如果存在一个正整数m与两个整数a,b，如果a-b能够被m整除，也就是说m|(a-b),那么a和b模m同余。记为：

模指数运算

模指数运算即先进行指数运算，之后再进行取模运算。例如：

在Python中给出了相应的处理函数（这在之后的使用Python进行编码求解相关问题的时候非常重要）：

pow(x，y，z)

函数是计算x的y次方，如果z存在，则再对结果进行取模，其结果等效于pow(x,y)%z注意：pow() 通过内置的方法直接调用，内置方法会把参数作为整型，而 math 模块则会把参数转换为 float。

欧几里得扩展算法

算法定义：对于不完全为0的非负整数a,b，gcb（a,b）表示a,b的最大公约数，必然存在整数对x,y使得gcd(a,b)=ax+by成立。

证明：

假设 a>b
　　1、显然当 b=0，gcd（a，b）=a，此时 x=1，y=0；
　　2、ab!=0 时，设 ax1+by1=gcd(a,b);
　　bx2+(a mod b)y2=gcd(b,a mod b);
　　根据朴素的欧几里德原理有 gcd(a,b)=gcd(b,a mod b);
　　则:ax1+by1=bx2+(a mod b)y2;
　　即:ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;
　　根据恒等定理得：x1=y2; y1=x2-(a/b)*y2;
    这样我们就得到了求解 x1,y1 的方法：x1，y1 的值基于 x2，y2.

上面的思想是以递归定义的，因为 gcd 不断的递归求解一定会有个时候 b=0，所以递归可以结束。

扩展欧几里得的递归实现（C语言）：

int exgcd(int a,int b,int &x,int &y)
{ if(b==0) {    x=1; y=0; return a;  } int r=exgcd(b,a%b,x,y); int t=x; x=y; y=t-a/b*y; return r;}

注：扩展欧几里得算法是之后RSA在知晓p、q、e的情况下求解d的主要思维算法，请详细了解。

RSA的加密解密原理

RSA加密解密涉及元素

N：大整数N，我们称之为模数（modulus）
p 和 q ：大整数N的两个因子（factor）
e 和 d：互为模反数的两个指数（exponent）
c 和 m：分别是密文和明文，这里一般指的是一个十进制的数还有一个就是n的欧拉函数值，在求解d的时候常用

RSA算法密钥的产生

（1）选择两个满足需要的大素数p和q，计算n=p*q，，其中是n的欧拉函数值。

（2）选一个整数e,满足条件1<e<,且gcd(,e)=1。通过，计算出d.

（3）以{e,n}为公开密钥，{d,n}为秘密密钥。

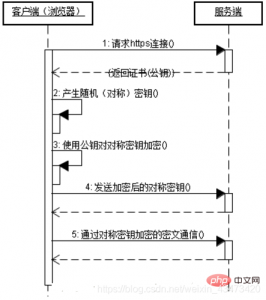
RSA加密解密原理图

公钥：{e,n} 私钥：{d,n}

简单的保密通信模型

模拟场景：

假设Alice是秘密消息的接收方，则只有Alice知道秘密密钥{d,n}，所有人都可以知道公开密钥{e,n}。

加密操作：

如果发送方发送需要保密的消息m给Alice,就选择Alice的公钥{e,n}，然后计算，之后把密文c发送给接收方Alice即可。

解密操作：

接收方Alice收到密文c之后,根据自己掌握的私钥计算,所得结果即为发送方要发送的消息。可以根据上面的“简单保密通信模型”来了解这一个过程。

RSA的安全性分析以及常用的攻击方法

通过上面的对RSA的加密解密的简单的解释与描述，可以知道，对于RSA加密解密算法而言，{e,n}为公开密钥，那么破解RSA最直接的方法就是分解整数n，计算n=p*q中的p与q的值，之后计算，通过即可求出d,之后使用{d，n}即可得出加密之前的明文。但是如果密钥的大小过大的话，那么就会产生“大整数分解难题”，从而导致解密失败。说完了“大整数分解难题”之后，下面就来简单的了解一些其他的影响RSA安全性的问题

如何保障RSA的安全性

（1）定期更换密钥

（2）不同的用户不可以使用相同的模数n

（3）p与q的差值要大，最好是差几个比特

（4）p-1与q-1都应该有大的素因子，一般建议选择的两个大素数p、q使得p=2p+1和q=2q+1也是素数。

（5）e的选择不可以太小，否则不安全哦。

（6）d的选择要慎重，不可以太小，一般要求满足。

针对RSA的攻击方法

（1）对模数n的因子分解

分解模数n是最直接的攻击方法，也是最困难的方法。攻击者可以获得公钥e和模数n，如果n=pq被成功分解，则攻击者可以计算出，进而从解得私钥d，之后即可进行解密。

CTF实战

题目来源： http://ctf5.shiyanbar.com/crypto/RSAROLL.txt

打开链接后我们可以看到给出了RSA加密之后的密文、加密所用到的e、n的值

按照我们之前所说的方法进行攻击测试：

首先分解模数n,这里我们可以采用在线分解模数的方法，推荐链接：http://www.factordb.com/index.php

之后我们可以得到分解后的p与q的值为18443 和49891

之后我们使用一个Python编写一个简易的脚本来求解d

import gmpy2
p =gmpy2.mpz(18443)
q =gmpy2.mpz(49891)
e =gmpy2.mpz(19)
phi_n= (p - 1) * (q - 1)
d = gmpy2.invert(e, phi_n)
print("d is:")
print (d)

得到d的值：d=96849619

经过上面的操作之后我们的到来p、q、e、d、n、c，那么接下来我就可以求解相应的明文了（将RSAROLL.txt中的{920139713,19}删除并且重新命名为rsa.txt保存在与Show_c.py同一目录下，之后执行以下操作）：

import gmpy2
n = 920139713
d = 96849619
result = []
with open("rsa.txt") as f:
for i in f:
        result.append(chr(pow(int(i),d,n)))

print(result)

成功得到最后的flag{13212je2ue28fy71w8u87y31r78eu1e2}

由以上可见，对于模数n的选取一定要慎重。

（2）对RSA的公共模数攻击

在上面的RSA的安全性保障中曾表名不同用户不可以使用相同的模数n，那么我们下面就来看看如果使用了相同的模数n会有什么情况发生。

若一个多用户系统中只采用一个模数n，不同的用户拥有不同的e和d，系统将是危险的。在此系统中，若用不同的公钥加密，这些公钥公模且互质，那么该信息无需私钥就可以解密。举例来说，设m为信息明文,两个加密公钥为e1和e2,公共模数是n，有

如果攻击者得到了n、e1、e2、C1、C2，就可以得到m，因为e1与e2互质，故用欧几里得算法能够找到x和y，满足，假设x为负数，需再使用欧几里得算法来计算则：

如果p<n，则p被获取。为了便于大家理解，下面做一个模拟场景来看看：

模拟场景：

假设一个公司采用了所有的公钥加密的同一条信息m，那么有以下结论：

此时有两个员工A与员工B，员工A持有密钥d1，他可以通过解密得到消息m。

同时员工B也可以使用其拥有的密钥d2来根据解密得到消息m。

如果此时有一个攻击者，同时监听了员工A、B接收到的密文C1和C2,因为模数不变，以及所有公钥都是公开的，那么利用同模攻击，他就可以在不知道d1、d2的情况下解密得到消息m.

CTF实战：

题目来源：Isc2016训练赛——PhrackCTF

下载题目中所给出的压缩包之后会发现里面有两个加密之后的文件flag.enc1和flag.enc2以及一个veryhardRSA.py的py文件，在veryhardRSA.py文件中给出了N的值、e1、e2的值，由此确定这个很是符合我们所提到的“公模攻击”

ISC2016给出了wirteup如下：

import gmpy2
def ByteToHex( bins ):
return ''.join( [ "%02X" % x for x in bins ] ).strip()
def n2s(num):
    t = hex(num)[2:]
if len(t) % 2 == 1:
        t = '0'+ t
return ''.join([chr(int(b, 16)) for b in [t[i:i+2] for i in range(0, len(t), 2)]])
n = 0x00b0bee5e3e9e5a7e8d00b493355c618fc8c7d7d03b82e409951c182f398dee3104580e7ba70d383ae5311475656e8a964d380cb157f48c951adfa65db0b122ca40e42fa709189b719a4f0d746e2f6069baf11cebd650f14b93c977352fd13b1eea6d6e1da775502abff89d3a8b3615fd0db49b88a976bc20568489284e181f6f11e270891c8ef80017bad238e363039a458470f1749101bc29949d3a4f4038d463938851579c7525a69984f15b5667f34209b70eb261136947fa123e549dfff00601883afd936fe411e006e4e93d1a00b0fea541bbfc8c5186cb6220503a94b2413110d640c77ea54ba3220fc8f4cc6ce77151e29b3e06578c478bd1bebe04589ef9a197f6f806db8b3ecd826cad24f5324ccdec6e8fead2c2150068602c8dcdc59402ccac9424b790048ccdd9327068095efa010b7f196c74ba8c37b128f9e1411751633f78b7b9e56f71f77a1b4daad3fc54b5e7ef935d9a72fb176759765522b4bbc02e314d5c06b64d5054b7b096c601236e6ccf45b5e611c805d335dbab0c35d226cc208d8ce4736ba39a0354426fae006c7fe52d5267dcfb9c3884f51fddfdf4a9794bcfe0e1557113749e6c8ef421dba263aff68739ce00ed80fd0022ef92d3488f76deb62bdef7bea6026f22a1d25aa2a92d124414a8021fe0c174b9803e6bb5fad75e186a946a17280770f1243f4387446ccceb2222a965cc30b3929
e1 = 17
e2 = 65537
s = gmpy2.gcdext(e1,e2)     #gmpy2.gcdext(e1,e2)的运行结果为元组(mpz(1), mpz(30841), mpz(-8))，所以元组的第0个值不能取，第1个值才是s1，第2个值由于是负数，所以要取反，变为正数
s1 = s[1]
s2 = -s[2]
file1 = open("veryhardRSA/flag.enc1" ,'rb').read()   #这里的路径要自己修改
c1 = int(ByteToHex(file1),16)
file2 = open("veryhardRSA/flag.enc2" ,'rb').read()   #这里的路径要自己修改
c2 = int(ByteToHex(file2),16)
c2 = gmpy2.invert(c2, n)        #由于根据前面的运算，s1是正数，s2是负数，后面需要运算c2的s2次幂。因为在数论模运算中，要求一个数的负数次幂，与常规方法并不一样，比如此处要求c2的s2次幂，就要先计算c2的模反元素c2r，然后求c2r的-s2次幂。
m = (pow(c1,s1,n) * pow(c2 , s2 , n)) % n
print(n2s(m))

执行之后得到最后的flag：

（3）对RSA的小指数攻击

如果RSA系统的公钥e选取较小的值，可以使得加密和验证签名的速度有所提高，但是如果e的选取太小，就容易受到攻击。

例如：使用同一个系统的三个用户，分别使用不同的模数n1,n2,n3，但是都选取e=3；另有一个用户欲将同一明文消息m发送给以上三人，使用个人的公钥加密得到：

一般情况下，n1,n2,n3互素，否则会比较容易求出公因子，从而安全性大幅度的减低，根据中国剩余定理，可以通过C1、C2、C3计算：

（4）RSA选择密文攻击

选择密文攻击是指攻击者能选择不同的密文，并拥有对应的明文，由此推出想要的信息。一般攻击者会伪装若干信息，让拥有四亚欧的用户签名，由此获得有用的明文-密文对，然后推算想要的信息，这一个工程量的大小要视情况而定。

CTF中的RSA的加密解密实战分析

可能涉及到的工具

（1）在线分解大素数：http://www.factordb.com/index.php；http://www.atool.org/quality_factor.php

（2）python的gmpy2、libnum包、以及一个python开发环境

（3）RSATools（Windows下的工具，这个在网上特别多可以随意找）（4）yafu:一个用于分解大整数的工具，可以运行与Windows平台上，语法简单易用操作。

附加：另外附加一个最近在GitHub上看到一一个非常不错的工具 CTF-RSA-tool，具体的使用方法在文档中读给出了相应的说明。下面是下载地址：https://github.com/D001UM3/CTF-RSA-tool

常见题型的分类

（1）已知p、q、e求解d

解题思路：根据这一欧拉函数式，可以使用所给的p、q求解出n的欧拉函数值,之后再根据即可求解出d的值。

CTF实例：

题目地址：http://www.shiyanbar.com/ctf/1828

解题步骤：

可以根据思路使用python进行编码实现：

import gmpy2
p =gmpy2.mpz(473398607161)
q =gmpy2.mpz(4511491)
e =gmpy2.mpz(17)
phi_n= (p - 1) * (q - 1)
d = gmpy2.invert(e, phi_n)
print("d is:")
print (d)

运行结果：

这一种题型较为直观，也是较为简单的一种。

（2）已知c、n、e求解明文

思路：根据可以对已知的n进行大数分解（可以使用在线工具，也可以使用python自己写脚本），之后得到p、q，之后根据，可以求解出n的欧拉函数值，之后根据，求解出d,最后可以根据经过编码求解出c，当然也可以使用RSAtools来操作。

CTF实例：

题目来源：IceCTF

打开链接之后可以看到给出了N、e、c的十六进制显示

思路：首先可以对N的十六进制进行转换，将其转换为十进制，之后使用yafu进行分解出p、q（此处在线分解无效，结果集太大），之后求解出d的值，并且将其转换为十六进制。在知道d、n、c的情况下就可以使用python进行编程求解最后的flag了：

解题步骤：

转十进制：

# encoding:utf-8
import gmpy2
n=int(0xee290c7a603fc23300eb3f0e5868d056b7deb1af33b5112a6da1edc9612c5eeb4ab07d838a3b4397d8e6b6844065d98543a977ed40ccd8f57ac5bc2daee2dec301aac508f9befc27fae4a2665e82f13b1ddd17d3a0c85740bed8d53eeda665a5fc1bed35fbbcedd4279d04aa747ac1f996f724b14f0228366aeae34305152e1f430221f9594497686c9f49021d833144962c2a53dbb47bdbfd19785ad8da6e7b59be24d34ed201384d3b0f34267df4ba8b53f0f4481f9bd2e26c4a3e95cd1a47f806a1f16b86a9fc5e8a0756898f63f5c9144f51b401ba0dd5ad58fb0e97ebac9a41dc3fb4a378707f7210e64c131bca19bd54e39bbfa0d7a0e7c89d955b1c9f)
print("n转换为十进制显示为：")
print(n)

分解大整数：

求解d,并且转换十六进制（在第一步的代码之后跟着写就行，不必新建文件）：

# encoding:utf-8
import gmpy2
n=int(0xee290c7a603fc23300eb3f0e5868d056b7deb1af33b5112a6da1edc9612c5eeb4ab07d838a3b4397d8e6b6844065d98543a977ed40ccd8f57ac5bc2daee2dec301aac508f9befc27fae4a2665e82f13b1ddd17d3a0c85740bed8d53eeda665a5fc1bed35fbbcedd4279d04aa747ac1f996f724b14f0228366aeae34305152e1f430221f9594497686c9f49021d833144962c2a53dbb47bdbfd19785ad8da6e7b59be24d34ed201384d3b0f34267df4ba8b53f0f4481f9bd2e26c4a3e95cd1a47f806a1f16b86a9fc5e8a0756898f63f5c9144f51b401ba0dd5ad58fb0e97ebac9a41dc3fb4a378707f7210e64c131bca19bd54e39bbfa0d7a0e7c89d955b1c9f)
print("n转换为十进制显示为：")
print(n)

e=gmpy2.mpz(int(0x10001))
p=57970027
q=518629368090170828331048663550229634444384299751272939077168648935075604180676006392464524953128293842996441022771890719731811852948684950388211907532651941639114462313594608747413310447500790775078081191686616804987790818396104388332734677935684723647108960882771460341293023764117182393730838418468480006985768382115446225422781116531906323045161803441960506496275763429558238732127362521949515590606221409745127192859630468854653290302491063292735496286233738504010613373838035073995140744724948933839238851600638652315655508861728439180988253324943039367876070687033249730660337593825389358874152757864093
phi_n=(p-1)*(q-1)
d=hex(gmpy2.invert(e, phi_n))
print("d的十六进制值为：")
print(d)

求解明文

import math
N=0xee290c7a603fc23300eb3f0e5868d056b7deb1af33b5112a6da1edc9612c5eeb4ab07d838a3b4397d8e6b6844065d98543a977ed40ccd8f57ac5bc2daee2dec301aac508f9befc27fae4a2665e82f13b1ddd17d3a0c85740bed8d53eeda665a5fc1bed35fbbcedd4279d04aa747ac1f996f724b14f0228366aeae34305152e1f430221f9594497686c9f49021d833144962c2a53dbb47bdbfd19785ad8da6e7b59be24d34ed201384d3b0f34267df4ba8b53f0f4481f9bd2e26c4a3e95cd1a47f806a1f16b86a9fc5e8a0756898f63f5c9144f51b401ba0dd5ad58fb0e97ebac9a41dc3fb4a378707f7210e64c131bca19bd54e39bbfa0d7a0e7c89d955b1c9f
e=0x10001
d=0x9186c78d098af6815622ea9901cf84a89ead578a6dbdded7d7fc63531756239dc586501216fc2e4bd1a8cee7e62284d16d91195f356d733a52dff011ebc3bf1e5d62af54d0455ea2f6ec948f45f34931f5b0b4478b16c66951a95d2f069a6c8867a6bc673c8e40052a54dbc5c1aeacbbfae7cad150a4f41ef4a02b1c97d70636ae187ed3c45f2551696a6a1172ae4089e033fb4853057c0f1e227d71ccf24fb27073ca4fe4ac3744dfed2cd7763c47ac4ae4d42820a19d68961bc103bb9016197463875169d062b45807e2e86aa17fa65e3088cc75ef35f984d0ca92d4c9270c2e694eb1f5df16b7ebe32b5c1d26086d6aac5fe327288f2904cb54164db39151
c=0x3dbf00a02f924a70f44bdd69e73c46241e9f036bfa49a0c92659d8eb0fe47e42068eaf156a9b3ee81651bc0576a91ffed48610c158dc8d2fb1719c7242704f0d965f8798304925a322c121904b91e5fc5eb3dc960b03eb8635be53b995217d4c317126e0ec6e9a9acfd5d915265634a22a612de962cfaa2e0443b78bdf841ff901423ef765e3d98b38bcce114fede1f13e223b9bd8155e913c8670d8b85b1f3bcb99353053cdb4aef1bf16fa74fd81e42325209c0953a694636c0ce0a19949f343dc229b2b7d80c3c43ebe80e89cbe3a3f7c867fd7cee06943886b0718a4a3584c9d9f9a66c9de29fda7cfee30ad3db061981855555eeac01940b1924eb4c301
print(hex(pow(c,d,N))[2:-1].decode('hex'))

（3）已知p、q、e、c求解明文

思路：根据求解出n的值，之后再根据，求解出n的欧拉函数的值，之后再根据求解出d的值，之后再根据求解出明文信息即可！

CTF实例：
题目地址：http://www.shiyanbar.com/ctf/1979

解题步骤：

根据题目思路使用python编码如下：

import gmpy2
p =gmpy2.mpz(9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483)
q =gmpy2.mpz(11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407)
e =gmpy2.mpz(65537)
phi_n= (p - 1) * (q - 1)
n=p*q
d = gmpy2.invert(e, phi_n)
c=gmpy2.mpz(83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034)
m=pow(c,d,n)
print("Message is :")
print(m)

运行结果：

（4）已知c、e，求解明文

思路：可能很多人看到这个情形，会觉得不可能解出最后的明文结果，但是对于一些知晓python的Crypto库的人来说这个也许是可行的，通过调用Crypto库中的相关函数模块可以实现对n、e的求解，之后就可以依次进行对n、n的欧拉函数、p、q、d的求解，最后即可求解出明文信息m.

CTF实例：

题目地址：http://www.shiyanbar.com/ctf/1772

解题步骤：根据解题思路编写python代码如下：

获取n、e

from Crypto.PublicKey import RSA
public = RSA.importKey(open('public.pem').read())
n = long(public.n)
e = long(public.e)
print n
print e

运行结果：

可以看到n的位数过大，所以推荐使用yafu来进行分解（使用在线分解是可以，但是当位数过多的时候就不行了）：

之后得到p与q为：

p=258631601377848992211685134376492365269
q=286924040788547268861394901519826758027

到目前为止，我们获得了n、e、p、q、c,那么我们就可以求解私钥，之后就可以进行解密了

求解私钥（本代码引用自hackpanda）：

import sys
import math
from Crypto.PublicKey import RSA

keypair = RSA.generate(1024)
keypair.p = 258631601377848992211685134376492365269
keypair.q = 286924040788547268861394901519826758027
keypair.e = 65537
keypair.n = keypair.p * keypair.q
phi_n = long((keypair.p-1) * (keypair.q-1))

i = 1
while (True):
    x = (phi_n * i ) + 1
    if (x % keypair.e == 0):
        keypair.d = x / keypair.e
break
    i += 1

private = open('private.pem','w')
private.write(keypair.exportKey())
private.close()

运行之后查看private.pem中可以看到已有私钥产生

之后可以使用密钥进行解密

（5）特殊情况

在有些情况下你会发现有时候题目中给出的n的值使用在线大整数分解后虽然有结果，但是你看不全，比如下面的这个：

这时即便是使用yafu、msieve等也长时间无果，那么这个时候你就应该换一换思路，比如说：发现加密的指数比较小、采用了相同的模等等，之后联想一下针对RSA的一些攻击方法来破解，而不是长时间的去想如何实现分解这个数，有时候CTF中的一些题目也会出现一些脑洞题。对于CTF中常常出现的RSA题型而言，解题的思路非常重要，只要你懂的了解题的方法原理，那么在你会一门编程语言的基础之上你就非常容易通过编程进行求解该问题。（强烈推荐Python）

建议大家不要过于依赖于各种工具，最好还是多熟悉熟悉原理，同时使用python多多编程，这样收获到的会更多，而且在实践中你的CTF中的题型的攻破能力也越来越强。